Entre représentation et production du réel

Le dictionnaire commun propose plusieurs définitions du terme « modèle » :

1. Ce dont on doit imiter la structure pour un emploi adéquat de quelque chose,
2. Catégorie constituée par un ensemble de caractéristiques et servant à classer des faits ou des objets,
3. Représentation du fonctionnement de quelque chose,
4. Personne possédant une caractéristique donnée à un très haut niveau,
5. Chose, animal ou personne que l’artiste représente dans son œuvre,
6. Objet qu’on imite pour fabriquer d’autres objets.

Ces différentes définitions font ressortir les deux conceptions courantes de la notion de modèle, correspondant à des visions presque antagonistes dans leur rapport au réel. La conception la plus évidente considère le modèle comme une représentation d’un objet : on peut penser à une maquette d’avion ou de bateau, qu’on appelle modèle réduit. Dans une logique d’induction (de l’objet vers le modèle), ce type de modèle est en effet une réduction du réel au sens où, pour reproduire et mimer l’objet réel, un certain nombre d’éléments et détails techniques ont été éliminés pour ne conserver que les aspects strictement nécessaires à la reconnaissance de l’objet. Dans cette première conception, le modèle relèvera de la mimésis platonicienne, et sera considéré à un rang inférieur vis-à-vis du réel selon le rapport hiérarchique qu’établit Platon dans les livres II et III de La République.

La seconde conception considère le modèle comme un objet à partir duquel il sera possible de produire des représentations. Un exemple immédiat est celui d’un dessin de nu et de son modèle. Il est intéressant de noter ici la distinction entre : 1) la personne dont le métier est d’être modèle (modèle en soi), et 2) une position particulière prise par le modèle qui semble instancier un modèle en tant que modèle d’un dessin ou d’une sculpture. Mais c’est également cette conception du modèle qui désignerait un plan d’architecture, à partir duquel les différents corps de métier vont travailler pour réaliser un bâtiment, ou, pour revenir à l’aéronautique, un modèle d’avion dans une soufflerie pour simuler l’écoulement de l’air sur la carlingue. Dans ces deux derniers exemples, le modèle participe à la réalisation d’un objet dont il est une abstraction. On retrouve ce principe de réduction propre à la notion, mais en en inversant le principe logique, à savoir une logique de déduction du modèle vers l’objet. Il relèvera alors d’une production du réel davantage que d’une représentation du réel.

Le modèle porte ainsi une dualité de sens, ce qui suggère que le modèle puisse se positionner comme une instance intermédiaire entre le réel et sa représentation, ou entre deux états du réel, et de manière plus générale, entre une intention et sa réalisation dans le réel.

Modèle descriptif / modèle prédictif

En informatique, cette dualité est connue, puisqu’on distingue les modèles descriptifs (du réel vers le modèle) et les modèles prédictifs (du modèle vers le réel). Dans le premier cas, il s’agit de représenter des données dites « historiques » : on peut penser comme exemple de modèle descriptif à une carte géographique ou à une comptabilité, qui est un modèle possible pour décrire les activités d’une entreprise. Pour le modèle prédictif, des variables connues, dites « explicatives », vont être utilisées pour déterminer des variables inconnues, dites « à expliquer ». Un exemple typique est le modèle météorologique¹ qui tente de prévoir la météo de demain à partir de la météo d’aujourd’hui.

Dans les deux cas, le modèle est à nouveau conceptualisé comme une réduction. C’est la simplification d’un fait, d’un objet, d’une réalité à modéliser ou à simuler, en une série limitée de paramètres et de relations. C’est donc le résultat d’une sélection des variables, procédant d’un choix sur les éléments à conserver dans le modèle, sur la base de leur pertinence pour une visée informatique ou scientifique.

Un concept aristotélicien

De ce point de vue, le modèle s’inscrit parfaitement dans le paradigme aristotélicien de la mimésis. Aristote parle de la poétique comme d’une organisation sensée du monde, une sélection (qui consiste à écarter les détails non intéressants et à conserver les détails pertinents). La poïesis semble ainsi procéder d’une expression symbolique du monde, et le modèle, à sa manière, d’une rationalisation du monde.

Mais on peut également relier au modèle le concept aristotélicien de dunaton (δυνατόν). On perçoit en effet dans le modèle une capacité contenue, une puissance. Parce qu’il est susceptible de générer une production d’un artefact dans le monde réel, le modèle est en puissance cet artefact. Et de ce point de vue, le modèle possède, comme la poésie dans la pensée d’Aristote, une valeur en soi qui ne dépend pas de ce qu’il modélise, et qui ne doit être valorisé par rapport à ce dont il est le modèle, mais par rapport à ce qu’il permet générer, de produire ou de simuler. L’absence de hiérarchie entre réalité et mimésis chez Aristote fonctionne également très bien avec la notion de modèle.

Un concept valéryen

De même, on peut rapprocher le modèle du mouvement et de l’imaginaire tels que Paul Valéry les pense, c’est-à-dire ancrés dans le réel et dans sa construction, plutôt que du côté de la pensée abstraite. Le modèle, tout comme la fonction géométrique de l’architecte, est de l’ordre du virtuel, de l’écriture du mouvement. Le modèle relève alors d’une écriture performative, en cela qu’il est source de possibles avant d’être une simple réduction du présent.

« Mais ta main, cependant, n’est plus libre d’errer sur le mur ; à présent, “tu veux” quelque chose, et tu imposes à ton tracement cette loi extérieure : qu’il reproduise une forme donnée. Tu t’obliges à ceci, et même tu as défini cette loi que tu t’es imposée, par ces quelques mots “représenter l’ombre de la tête de Socrate sur une surface plane” Cette loi n’est pas suffisante pour guider ta main, puisqu’il y faut encore la présence du modèle ; mais elle régit l’ensemble de son action ; elle en fait un tout, qui a sa fin, sa sanction, et ses bornes. » (Valéry 1921, Eupalinos ou l’architecte)

Dans cet extrait, Paul Valery met en évidence la puissance de l’intention, et sa rencontre avec un modèle, ici au sens du modèle d’un artefact en puissance. Cette prévalence de l’intention sur le modèle se retrouve tant en informatique qu’en sciences en général pour lesquels la modélisation et la sélection de variables pertinentes dépendent principalement des objectifs, c’est-à-dire de l’intention initiale.

Vecteur de la conversation scientifique

Au-delà de ces acceptations de la notion dans le langage courant, le modèle est également au cœur de l’activité scientifique, et ce dans tous les domaines de recherche : du modèle physique de la gravité, qui, une fois exprimé dans une forme mathématique, nous permet de prévoir la trajectoire d’un projectile, au modèle chimique d’une solution gazeuse qui permet d’effectuer des expérimentations sans même posséder cette solution gazeuse, en passant par le modèle conceptuel du structuralisme.

Jean-Guy Meunier rappelle son rôle heuristique essentiel dans le processus de la pensée scientifique :

« Le rôle cognitif que les modèles jouent dans une théorie scientifique est original. Ils assistent la théorie dans la multiplicité et la diversité de leurs tâches et leurs objets de recherche, par exemple : la conception de la problématique, la formulation des hypothèses, l’intégration aux recherches existantes, la définition de la méthode, l’introduction d’une formalisation, l’illustration par la simulation, la construction de prototypes, le design de l’expérimentation, l’interprétation et la dissémination des résultats, etc. » (Meunier 2017)

Cette « assistance » au chercheur confère en fait au modèle une position centrale dans le travail scientifique, conformément à cette formule attribuée à Paul Valéry : « nous ne raisonnons que sur des modèles »².

Dans son article La modélisation et la simulation des objets et processus complexes (Pavé 2005), Alain Pavé explicite comment le modèle, par itérations successives, participe du processus d’acquisition des connaissances.

« Dans l’activité de recherche, pouvoir le mettre en défaut, pouvoir le réfuter, soit par l’expérience, soit par les observations est son intérêt premier. C’est lorsqu’il “ne marche pas” qu’on acquiert de la connaissance. Alors, il est loisible de le modifier et de vérifier que la modification est à nouveau en adéquation avec les données. Ainsi se met en place la boucle vertueuse, maintenant bien connue, associant expérimentation ou observation, modélisation et simulation qui permet d’avancer dans le processus d’acquisition des connaissances. »

Pavé confirme surtout le rôle central de médiation du modèle dans le champ scientifique, en cela qu’il est communicable, reproductible et ainsi vérifiable. Il devient de fait le point focal de la conversation scientifique, de la controverse ou de la validation par les pairs.

« Le modèle est un objet précieux pour l’acquisition des connaissances, mais aussi pour le dialogue entre scientifiques. Il peut même être un trait d’union entre disciplines. »

Pragmatisme

L’histoire des sciences fait apparaître des conceptions divergentes du savoir et de son élaboration. Les notions de réel, ou de vérité sont ainsi travaillées par des perspectives radicalement différentes selon les écoles de pensée et les paradigmes qui les sous-tendent.

Creswell synthétise trois de ces paradigmes dans le tableau suivant (Creswell 2003) :

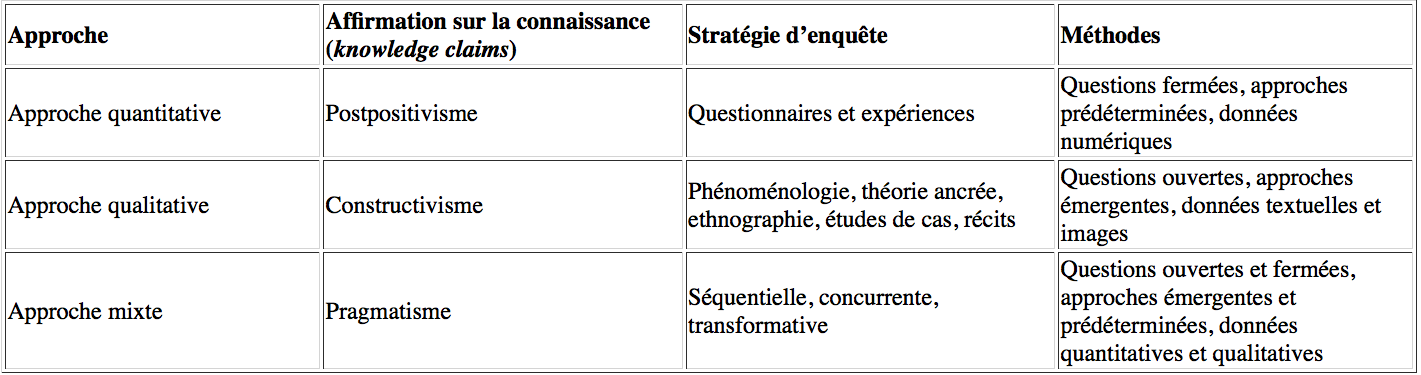
On retrouve les fondements de cette classification chez Meunier (2017) lorsqu’il identifie les différentes compréhensions de la notion de théorie selon les paradigmes scientifiques. Ainsi, la théorie scientifique change de nature selon des « visions » que Meunier qualifie pour sa part de syntaxique, sémantique ou pragmatique. La première, qui relève du positivisme logique conçoit la théorie comme « un ensemble d’énoncés formés par des règles strictes et dont certains sont soit des théorèmes, soit des axiomes ou des postulats ». La seconde vision, dite sémantique, ajoute à la syntaxe mathématique de la théorie une expression sémantique propre à un domaine de recherche. Enfin, la vision pragmatique vient dépasser les deux premières (syntaxique et sémantique) en cela qu’elle n’hésite pas à considérer la théorie comme dynamique, constamment travaillée par des formes de discours et des approches différentes :

« Dans cette vision, une théorie est vue comme un moment, un état de stabilisation d’un processus cognitif complexe souvent itératif et qui s’exprime sous diverses formes sémiotiques et discursives, formelles ou non formelles, ou même iconiques (graphes, les plans, les simulations, etc.). » (Meunier 2017)

Cette hétérogénéité des formes rappelle les méthodes mixtes telles que définies par Creswell qu’il associe au pragmatisme en cela qu’elles articulent une approche quantitative de la science, associée au (post-)positivisme, et une approche qualitative associée au constructivisme.

La suite de la citation de Meunier est intéressante, car c’est le modèle qui vient réunifier et articuler (de manière « pragmatique ») les différentes approches d’une problématique :

« Ce processus cognitif réunit en fait divers points de vue, perspectives, et stratégies d’enquête, démonstrations, langages, etc., portant sur les phénomènes étudiés. Chacun de ses points de vue, angles, perspectives, intérêts et que l’on regroupe dans cette vision pragmatique sous le terme englobant de “modèle”. »

Formalisation des sciences

Entre le chercheur et le monde qu’il cherche à comprendre, une médiation technique s’est constamment imposée. Que ce soit les premières lentilles d’observation du ciel ou du microscopique, ou le papier et l’écriture pour dessiner, décrire, ou même extérioriser une pensée, cette médiation assure un nécessaire décalage entre le réel et les perceptions naturelles de l’observateur. Les modèles sont en quelque sorte des états un peu plus avancés de cette médiation, dans le sens notamment d’une formalisation et d’une généralisation.

La formalisation mathématique notamment s’est progressivement imposée aux disciplines dites « dures » au fur et à mesure qu’avançaient les progrès de la discipline « reine ». Les mathématiques ont en effet permis aux autres disciplines de se désolidariser du réel (c’est-à-dire des phénomènes et manifestations physiques) et de découvrir de nouvelles connaissances à partir de leurs seuls calculs. Avec la complexification des mathématiques à la fin du XIX^ème siècle, les scientifiques décrivent le non perceptible et progressent dans l’infiniment petit (découvertes de nouveaux éléments) et l’infiniment grand (constitution des astres), démontrent le principe de la relativité, remontent le temps (cosmologie).

Ces disciplines n’auront de cesse ensuite de revenir à l’observation pour vérifier ces théories à l’état de modèle, et apporter, après la preuve mathématique, la preuve sensible d’une connaissance. Une des plus grandes découvertes de ces dernières années, les ondes gravitationnelles, n’est ainsi que la confirmation d’une théorie déjà centenaire.

À ce propos, la complexité des médiations techniques permettant d’observer ces phénomènes n’a cessé de croître. Les lentilles, les tracés sismographiques, les solutions colorées, encore à portée de la perception humaine, ont été remplacés par des capteurs, pour la plupart numériques, dont les données récoltées ne sont elles-mêmes intelligibles qu’à travers de nouvelles médiations, souvent complexes. Ces médiations successives ne sont évidemment pas neutres et posent de réelles problématiques épistémologiques aux équipes qui les emploient Sauvage et al. (2014). Que ce soit dans l’infiniment petit avec les microscopes à balayage électronique, ou les télescopes comme Herschel³, les images données à voir sont de pures constructions relevant davantage de la vue d’artiste que d’une quelconque réalité.

L’introduction de l’informatique dans les pratiques scientifiques a généré une nouvelle vague de formalisation, notamment dans les procédures de calcul et de traitement. Elle a ainsi ajouté une modélisation supplémentaire dépendante des couches logicielles, que ce soient les langages de programmation ou les langages de base de données. Par exemple, la modélisation informatique de la trajectoire d’Apollo 11 en 1969 ne pourrait être équivalente à la modélisation informatique de la même trajectoire en 2017. Les technologies ont changé, aussi bien dans le choix de langage, la modélisation de ces dernières, ou encore l’encodage numérique des données.

La modélisation mathématique se double ainsi d’une modélisation informatique, préalable à une manipulation et à la computation du modèle initial par le processeur. La transposition d’un modèle à l’autre peut sembler relativement indolore pour les disciplines de sciences dures, qui ont su exprimer de plus en plus finement les phénomènes observés en systèmes formels⁴. Cependant, il en est autrement pour les sciences humaines. Si elles ont toujours su élaborer des modèles pour exprimer leurs connaissances, leur formalisation mathématique, et de surcroît informatique, se heurte à plusieurs obstacles.

Les trois formes de modèles

Pour Meunier (2014), l’utilisation de l’ordinateur dans l’activité scientifique fait intervenir trois modélisations distinctes, autorisant le passage d’un niveau conceptuel à un autre de manière transitive. Dans cet article de 2014, Meunier reprend une taxonomie inspirée des travaux de Dennet (1978), Pylyshyn (1984) et Marr (1982), et distingue :

1. la modélisation intentionnelle ou représentationnelle, qui exprime les objets et les tâches à effectuer sur ces objets en utilisant des concepts issus du discours ordinaire. Il s’agit d’une représentation.
2. la modélisation fonctionnelle, traduit ces objets et tâches en termes d’intrants et de fonctions. Ces fonctions doivent être computables.
3. la modélisation physique ou matérielle, présente les mécanismes de la machine qui réalisent les fonctions physiquement. Dans le cas de l’ordinateur, la matérialité de la machine est bien sûr électronique, mais on parle bien de modélisation physique dans le sens où une machine réalise concrètement (ou mécaniquement⁵) une suite de calcul.

Reprenons alors l’exemple de Paul Valéry et voyons comment pourraient s’exprimer ces trois modèles :

La première modélisation est l’expression du problème en langage socratique (ou valéryen). La seconde est la traduction du problème en fonction mathématique, celle-là même dont Valéry (1921) faisait l’éloge. Enfin, la dernière consiste ici en une traduction du problème en code informatique⁶, à titre démonstratif comme une instance de modélisation informatique.

Cette taxonomie évolue d’un article de Meunier (2014) à l’autre Meunier (2017). Des modélisations intentionnelle, fonctionnelle et physique, héritées d’une catégorisation de « postures » ou de points de vue, Meunier adopte sa propre taxonomie et déplace son objet sur les modèles eux-mêmes, identifiant alors les modèles conceptuel, formel et matériel.

Cependant Meunier insiste : toute recherche utilisant l’ordinateur comme machine computationnelle, devrait, pour justifier la validité des recherches, être en mesure d’exprimer ces trois modélisations et de montrer leur transitivité, en particulier dans le champ des humanités où le passage du conceptuel au formel est trop souvent mal maîtrisé.

Modèle formel computationnel

Meunier (2017) décrit le modèle formel ainsi :

« Un modèle sera dit formel si les formes sémiotiques qu’il contient sont un ensemble de symboles strictement régis par des règles. Par commodité, on appellera souvent ces systèmes symboliques formels des langues formelles où les symboles de départ constituent un vocabulaire et les règles définissent une syntaxe. Ce langage est sans sémantique. Cependant un modèle formel sera dit interprété si dans une application à un domaine spécifique, une sémantique lui est ajoutée. »

Ainsi, la principale caractéristique du modèle formel est d’être essentiellement syntaxique, ce qui est par ailleurs une condition sine qua non pour être computationnel.

Un modèle formel est dit computationnel lorsqu’il est calculable ou décidable. Meunier rappelle que cette computationnalité est équivalente à la calculabilité (Soare 2009), elle-même définie comme une manipulation formelle de symboles (soit aussi une manipulation purement syntaxique et dépourvue de signification) consistant à déterminer si une équation appartient ou pas à un système mathématique. L’équivalence entre calculabilité et computationnalité est démontrée grâce à la machine de Turing, dont la nature physique et mécanique prouve la faisabilité du calcul (Soare 2009; Turing 1937). L’ordinateur peut alors être considéré sommairement comme une instanciation de la machine de Turing dans une machine électronique.

On ne fera que nommer ici les propriétés d’une fonction computationnelle : récursive, algorithmique et combinatoire, ou encore exprimées autrement par certaines sources : atomicité, systématicité et productivité. Une fonction possédant ces trois propriétés est de fait un système formel de nature essentiellement syntaxique : la sémantique des fonctions leur est externe. Autrement dit, le calcul peut être effectué par une machine, mais son interprétation n’est pas possible par la machine. La machine ne comprend pas de quoi on parle, quand bien même une sémantique serait « attachée » aux symboles.

Par ailleurs, on retiendra que même si on fournit à la machine des 0 et des 1 (système sémiotique particulier) pour exprimer un objet ou une fonction (autre système sémiotique), cela ne suffit pas à rendre ces fonctions computationnelles. Être numérique n’est pas une condition suffisante (ni nécessaire) de la computationnalité. De fait, il existe en mathématique une infinité de fonctions non computables, ou non calculables, tandis qu’il existe un sous-ensemble de fonctions computables très restreint au regard de l’ensemble des fonctions (Soare 2009; également Meunier 2014).

Finalement, le numérique, bien qu’il se traduit dans une représentation sémiotique, ou un encodage formel, n’est pas nécessairement un système formel, ni par extension un système computationnel.

Modéliser les humanités ?

Ainsi, notre question initiale : « les humanités sont-elles solubles dans le numérique ? » deviendrait plutôt : « les humanités sont-elles solubles dans un modèle formel computationnel ? ». Ce à quoi Meunier (2017) répond :

« il n’y a pas d’humanités dites numériques s’il n’y a pas de modélisation formelle contenant des systèmes symboliques mathématiques calculables traduisibles en algorithmes. Bref, tout projet sérieux dans les Humanités numériques, parce qu’utilisant l’ordinateur, met en place implicitement ou explicitement une modélisation formelle. »

Cependant, la question de savoir si les objets sémiotiques d’étude des humanités sont modélisables en modèles calculables est légitime étant donnée la complexité intrinsèque des objets d’étude. En effet, les humanités se penchent sur des objets de nature sémiotique : c’est-à-dire que leur qualité première n’est pas d’être dénombrable ou quantifiable, mais c’est d’avoir une signification (et en fait une multiplicité de significations). La sémioticité des données ne permet pas d’assurer leur atomicité, qui est une des propriétés nécessaires à la computabilité de la fonction (Meunier 2014).

Cette multiplicité de sens a nécessairement pour conséquence une multiplicité de modèles, chacun traversé de positions théoriques, de choix culturels, et susceptibles de produire des résultats différents. Mais alors, est-ce qu’un modèle subjectif, « multiple », peut encore jouer son rôle de modèle  ? Est-il transposable à d’autres questions de recherche, à d’autres corpus, etc. ? En multipliant les modèles (un modèle par objet d’étude et potentiellement un modèle par chercheur), n’entrave-t-on pas sa fonction de vecteur de conversation scientifique ?

Les humanités, qu’elles soient numériques ou non, ne peuvent faire abstraction de leur subjectivité de point de vue, et de leur singularité d’interprétation.

La proposition de Meunier consiste alors à considérer les modèles comme des formes incomplètes de l’objet d’étude, des formes purement syntaxiques, mais auxquelles ont peut associer une sémantique. Ces modèles ne répondent pas aux problématiques d’ordre herméneutique que posent les chercheurs sur leurs objets, mais ils participent à l’interprétation en l’outillant et en fournissant de nouvelles données (calculées) sur l’objet d’étude. Il considère ainsi que l’ordinateur doit se positionner correctement dans la chaîne des opérations interprétatives réalisées par les chercheurs en humanités. Autrement dit, tout résultat d’une computation, d’un modèle, reste à interpréter pour acquérir une valeur scientifique du point de vue des humanités. Le résultat syntaxique des calculs reste une représentation ou une simulation du modèle, une vue de l’ordinateur dont l’interprétation produira une vue de l’esprit. Seule cette dernière étape peut intégrer les biais culturels, les choix et les sélections du modèle.

Cette interprétation des résultats revient en fait à la maïeutique qui permet de décrire souvent le travail du chercheur sur des données informatiques. On parle de « dialogue » entre le corpus et le chercheur, entre le monde et le chercheur. Dans ce dialogue monde-chercheur, on peut apercevoir la médiation croisée entre modèle et machine (la machine opérant et performant le modèle), porteurs ensemble d’un couple requête-résultat encore à interpréter.